import numpy as np
import pandas as pd
import matplotlib
import matplotlib.pyplot as plt
import seaborn as sns6 Modelle bewerten
Wie gut ist mein Neuronales Netz (Modell) und nach welchen Kriterien kann ich die Güte messen? In diesem Kapitel beschäftigen wir uns mit der Evaluation von Modellen und den entsprechenden Metriken Recall, Precision und Accuracy. Zudem lernen wir die Methode der Cross-Validierung kennen, wo wir den “Verlust” von Trainingsdaten durch das Freihalten von Testdaten minimieren.
True/False Positives/Negatives, Konfusionsmatrix, Recall, Precision, Cross-Validierung, Leave-One-Out
Nach Abschluss des Kapitels können Sie:
- Methoden zur Evaluation von Vorhersagemodellen erklären, sowohl für binäre als auch für Mehrklassen-Klassifikation, inklusive relevanter Begriffe wie True/False Positives etc.
- Konfusionsmatrizen interpretieren und die Metriken Recall, Precision und Accuracy ihre Unterschiede erklären, berechnen und anwenden
- mit Hilfe der Metriken die Güte von Modellen für eine Problemstellung bewerten
- die Methoden Cross-Validierung und Leave-One-Out erklären
Importe
6.1 Evaluation von Modellen
Wie bewerten wir die Güte eines trainierten Modells? Bei der linearen Regression haben wir den mittleren quadratischen Fehler (MSE) als Maß genommen, beim Perzeptron die Summe der quadratischen Fehler (SSE). Diese Maße messen ja den numerischen Abstand zwischen der gewünschten Ausgabe und der berechneten Ausgabe.
Bei Klassifikationsproblemen messen wir ein Modell daran, wie oft eine Klasse richtig bestimmt wurde, egal wie groß der Abstand der darunter liegenden Berechnung war (dieser spielt beim Lernprozess eine Rolle, aber nicht bei der finalen Evaluation).
Wir unterscheiden zwischen binärer Klassifikation und Klassifikation mit drei oder mehr Klassen. Wir beginnen mit binärer Klassifikation.
6.2 Binäre Klassfikation
Bei der binären Klassifikation erstellen wir ein Modell, dass eine Klasse K errechnen können soll. Das heißt, die Ausgabe ist K oder nicht K. Eine solche Klasse kann zum Beispiel “Katzenbild” sein und entsprechend “kein Katzenbild”. Ein weiteres Beispiel wäre Corona, wo wir unterscheiden zwischen “hat Corona” und “hat kein Corona”.
Es gibt dazu einen schönen Artikel auf Wikipedia
In der Coronazeit hat das ZDF ein Video mit dem Beispiel “Corona-Schnelltest” produziert: Wie zuverlässig sind Corona-Schnelltests?. Überlegen Sie gern, mit welchen der hier vorgestellten Maße die im Video gezeigten Maße übereinstimmen.
6.2.1 Positives und Negatives
Alle Trainingsbeispiele, die von Typ K sind, nennen wir Positives, alle anderen Negatives. Im Corona-Beispiel teilen wir unsere Population in Positives und Negatives ein:
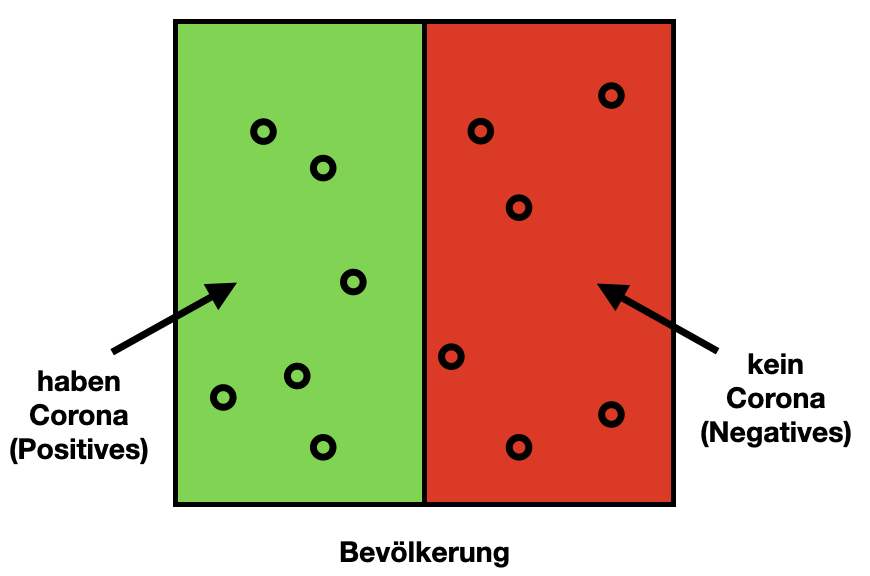
Wenn wir alle Trainingsbeispiele durch unser Modell schicken, erhalten wir jedes Mal eine errechnete Klasse (engl. predicted class) und kennen natürlich auch die echte Klasse (engl. actual class).
Im Corona-Beispiel können wir uns einen Corona-Schnelltest als Modell vorstellen. Die Population besteht jetzt aus allen per Schnelltest getesteten Personen (zum Beispiel für eine Teststation in einem bestimmten Zeitraum mit einem Test pro Person).
Der Schnelltest definiert eine Treffermenge (Kreis). Alle Personen in der Treffermenge sind gemäß des Tests positiv.
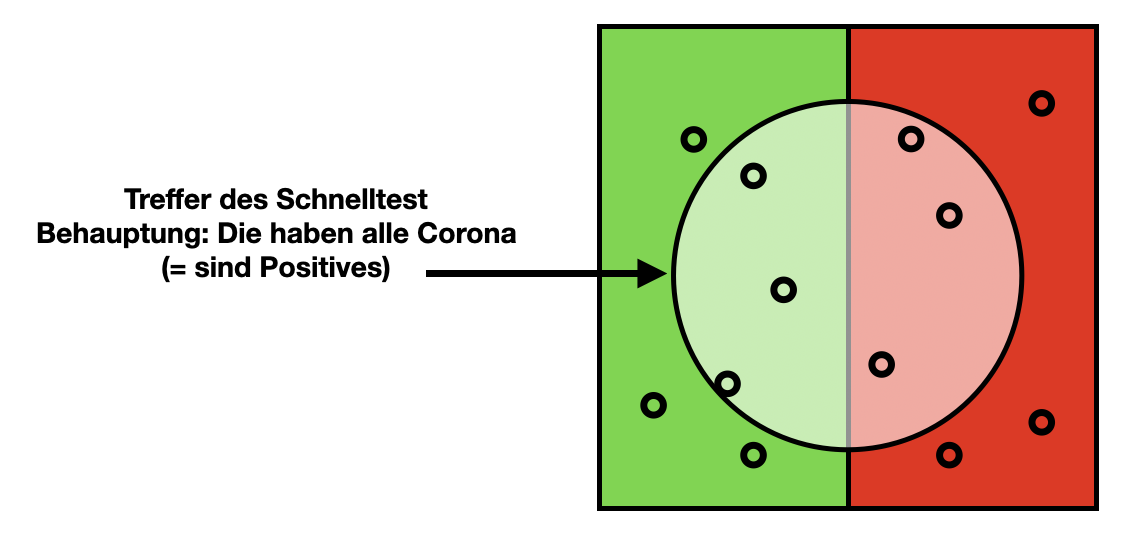
(Die grafische Darstellung ist von den Wikipedia-Eintrag inspiriert: https://en.wikipedia.org/wiki/Precision_and_recall)
6.2.2 True Positives und False Positives
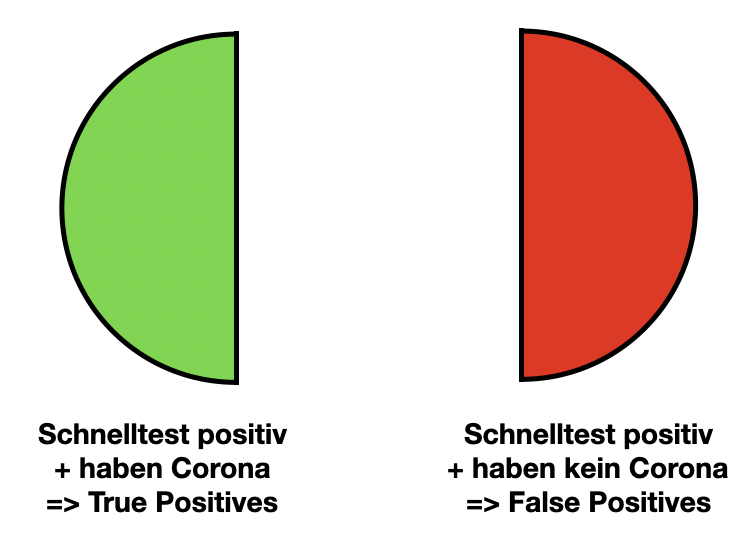
Jetzt unterscheiden wir vier Fälle. Zunächst schauen wir uns die Treffermenge an (die, die positiv getestet wurden). Hier unterscheiden wir zwischen Tests, die korrekterweise positiv sind, da die Personen Corona haben (True Positives) und solchen Tests, die fälschlicherweise behaupten, die Person sei positiv, obwohl sie kein Corona hat (False Positives).
- True Positives (TP): Anzahl der Samples, die korrekterweise K zugeordnet wurden
- False Positives (FP): Anzahl der Samples, die als K erkannt wurden, obwohl sie nicht zu K gehören
Die False Positives sind also “falscher Alarm” und führen beim Beispiel Corona dazu, dass (unnötigerweise) Quarantäneregelungen greifen.
6.2.3 True Negatives und False Negatives
Jetzt schauen wir uns die Tests an, die außerhalb der Treffermenge sind. Auch hier haben wir Tests, die korrekterweise außerhalb der Treffermenge sind, weil die Personen kein Corona haben (True Negatives), und solche, die fälschlicherweise negativ sind, da die Personen doch Corona haben (False Negatives).
- True Negatives (TN): Anzahl der Samples, die korrekterweise nicht K zugeordnet wurden
- False Negatives (FN): Anzahl der Samples, die als nicht K erkannt wurden, obwohl sie zu K gehören
Die False Negatives sind also diejenigen, die wir eigentlich suchen, aber die uns “durch die Lappen” gegangen sind. Im Fall von Corona heißt das: Diese Personen denken, sie seien nicht ansteckend, sind es aber doch!

6.2.4 Gesamtbild
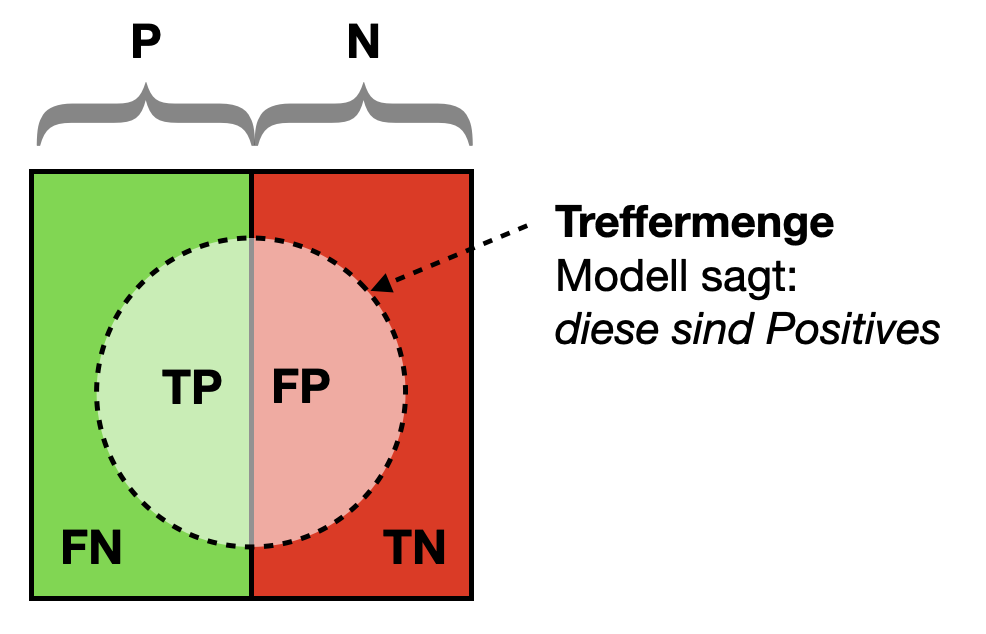
Wir schauen uns nochmal unser Diagramm an, weil wir dort schön alle Konzepte sehen.
Die gesamten Daten spalten sich in zwei Teile:
- P (Positives): Daten, die zu der gesuchten Klasse gehören, z.B. “ist Corona-inzifiert”
- N (Negatives): Daten, die nicht zur gesuchten Klasse gehören, z.B. “hat kein Corona”
Die Treffermenge sind solche Daten, die unser Modell für Positives hält. Sie besteht aus:
- TP (True Positives): Daten, die korrekt klassifiziert wurden, die unser Modell also korrekt “erkannt” hat
- FP (False Positives): Daten, die gar nicht zur Klasse gehören, aber vom Modell als Treffer zurückgeliefert wurden
Außerhalb der Treffermenge unterscheiden wir ebenfalls zwei Fälle:
- TN (True Negatives): Daten, die korrekterweise nicht als Treffer zurückgeliefert wurden, denn sie gehören nicht zur Klasse
- FN (False Negatives): Daten, die eigentlich in die Treffermenge gehören, die unser Modell aber nicht “erkannt” hat
6.2.5 Konfusionsmatrix
In einer Konfusionsmatrix (engl. confusion matrix) zählen wir bei jedem Trainingsbeispiel mit, von welcher Klasse (K oder nicht K) es ist und welche Klasse (K oder nicht K) das Modell errechnet hat. Jede Zelle der Konfusionsmatrix entspricht einem der vier oben genannten Fälle:
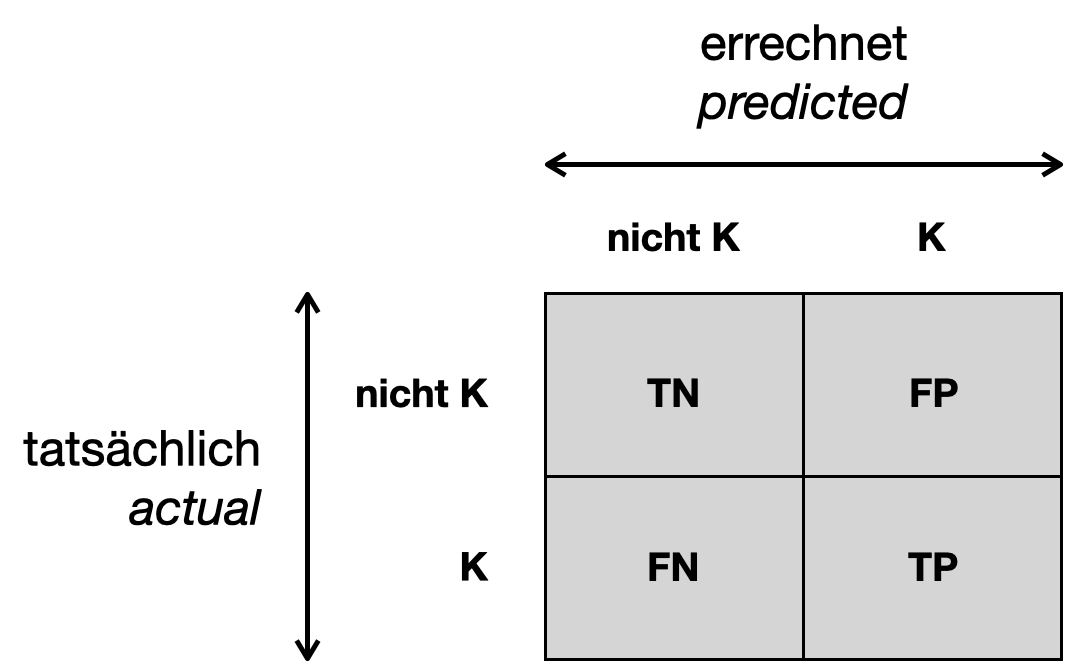
Die obere Zeile (d.h. Summe der zwei Zellen) entspricht allen Negatives, die untere Zeile allen Positives.
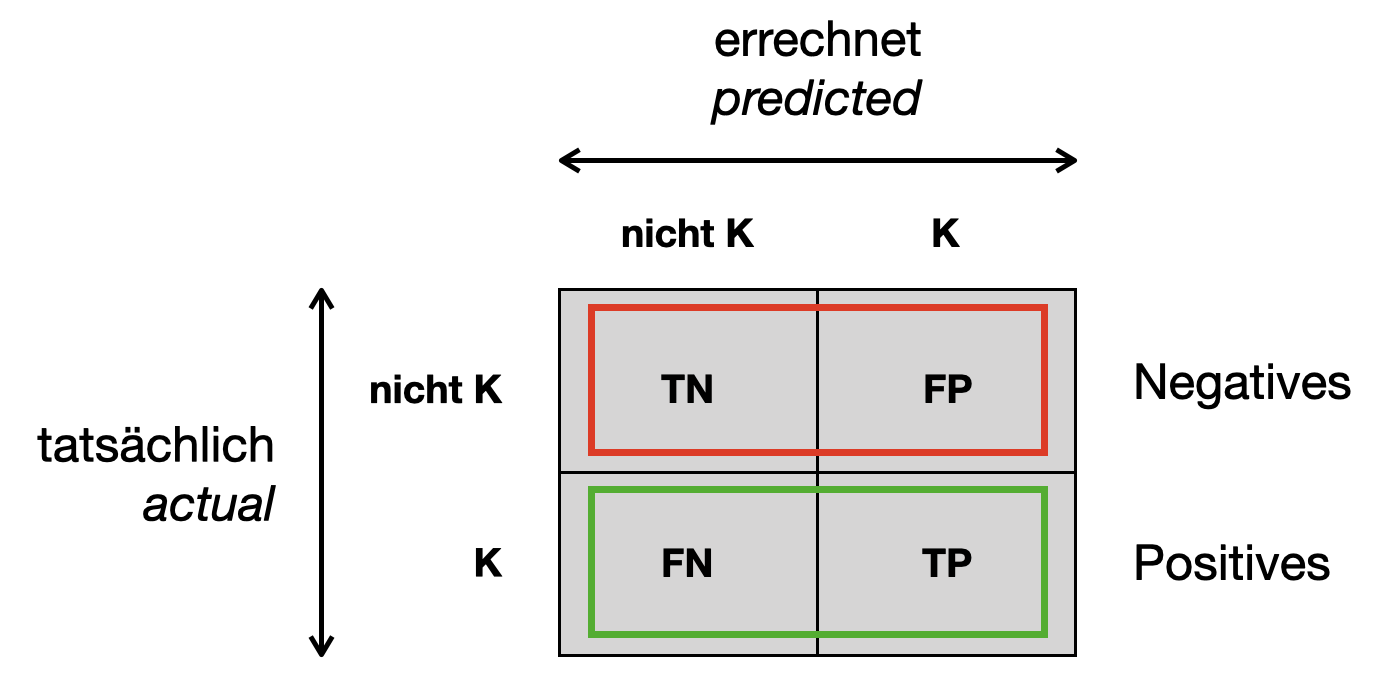
Auf der Diagonalen stehen alle korrekten Vorhersagen (TP + TN). Die anderen beiden Zellen sind die Fehlklassifikationen (FN + FP). Die Summe aller Zellen ist die Anzahl aller Trainingsbeispiele (TP + TN + FP + FN).

Hier ein Beispiel mit echten Zahlen. Jetzt nehmen wir ein Beispiel, wo wir Mails in SPAM und nicht-SPAM klassifizieren.
| nicht SPAM (predicted) | SPAM (predicted) | |
|---|---|---|
| nicht SPAM (actual) | 556 | 12 |
| SPAM (actual) | 4 | 28 |
Es handelt sich um 600 Trainingsbeispiele (Summe aller Zellen). Davon wurden 584 korrekt klassifiziert (Diagonale). Es gab 32 Samples der Klasse SPAM (untere Zeile). Das Modell hat aber 40 Samples als SPAM klassifiziert (rechte Spalte).
6.2.6 Recall
Die Metrik Recall misst, wie viele von allen möglichen Treffern wir “erwischt” haben. In anderen Worten: Wie viele Positives wir korrekt vorhergesagt haben (TP), relativ zu allen tatsächlichen Positives (TP + FN). Ein Corona-Beispiel: Von 100 Menschen sind 10 Corona-erkrankt; wenn 8 von diesen 10 einen positiven Corona-Test haben, dann hat diese Corona-Testmethode einen Recall von 80%. Wichtig ist auch, dass es egal ist, wie viele “Fehlalarme” wir hatten (FP).
Andere Bezeichnungen für Recall sind:
- Sensitivität
- True-Positive-Rate
- Trefferquote/Hit rate
Rechnerisch heißt das:
\[ \mbox{recall} = \frac{TP}{TP + FN} = \frac{TP}{P} \]
Im SPAM-Beispiel oben kommen wir auf einen Recall von 87.5%:
\[ \mbox{recall} = \frac{28}{28 + 4} = 0.875\]
6.2.7 Precision
Die Metrik Precision misst, wie viele von den Vorhersagen, die wir getroffen haben (TP + FP), wirklich korrekt waren (TP).
Ein Corona-Bespiel:
- Von 100 getesteten Menschen sind 10 Corona-infiziert (P = 10)
- 30 Tests zeigten positiv (TP + FP = 30)
- nur 8 der positiv getesteten waren wirklich Corona-infiziert (TP = 8)
Klingt ganz OK? Es gab immerhin 22x falschen Alarm (FP = 22). Und ein falscher Alarm bei einem Corona-Test ist unangenehm.
Das heißt, diese Corona-Testmethode hat (nur) eine Precision von 27%. Man kann in diesem Kontext auch sagen, Precision modelliert die Wahrscheinlichkeit, dass ein positiver Schnelltest auch wirklich stimmt.
Im Gegensatz zu Recall spielt es nur eine kleine Rolle, dass man eine große Menge der tatächlichen Fälle “erwischt” hat (wie oben im Beispiel 80%). Stattdessen geht es hier um das Verhältnis von echten Treffern zu falschen Alarmen.
Ein anderer Begriff für Precision ist Genauigkeit.
\[ \mbox{precision} = \frac{TP}{TP + FP} \]
Im SPAM-Beispiel kommen wir auf eine Precision von 70%:
\[ \mbox{precision} = \frac{28}{28 + 12} = 0.7\]
6.2.8 Bedeutung von Recall und Precision
Sie sollten sich anhand von Beispielszenarien klar machen, dass Recall und Precision sehr unterschiedliche Aspekte messen, die je nach Einsatzgebiet unterschiedlich wichtig sind.
Hoher Recall: Beim Beispiel Corona möchte man natürlich alle Infizierten auch positiv testen, also einen hohen Recall erzielen. Wie bekommen Sie einen hohen Recall? Ganz einfach: Ihr Schnelltest (Modell) schlägt immer positiv aus. Das ergäbe 100% Recall. Aber natürlich auch extrem viele False Positives. Ein fälschlich positiver Coronatest hat unangenehme Folgen (14 Tage Quarantäne oder ein PCR-Test mit Quarantäne, bis das Ergebnis da ist). Hier ist es sinnvoll, mit der Precision zu messen, wie zuverlässig ein Test ist.
Hohe Precision: Wenn Sie Ihren Schnelltest sehr vorsichtig gestalten und sehr selten positiv ausschlagen, wenn Sie absolut sicher sind, dass der Test positiv ist, dann erzielen Sie vielleicht eine hohe Precision. Aber oft entgehen Ihnen dann sehr viele der tatsächlichen Positives und der Recall ist niedrig.
Überlegen Sie sich für andere Szenarien (defekte Bauteile in der Produktion detektieren, gefährliche Situationen per Überwachungskameras identifizieren etc.), welche Bedeutung Recall und Precision haben.
6.2.9 Accuracy
Die Metrik Accuracy betrachtet die Gesamtmenge aller richtigen Vorhersagen (Diagonale der Konfusionsmatrix oder TP + TN) relativ zu der Gesamtzahl der Samples (Summe aller Felder der Matrix). Interessant ist, dass die beiden Klassen (z.B. Corona und Nicht-Corona) gleichberechtigt in die Rechnung eingehen, wohingegen Recall und Precision immer “aus Sicht” der Positivklasse konzipiert sind. Im Bereich der Neuronalen Netze ist Accuracy das Standardmaß, um einen Eindruck von der Modellgüte zu gewinnen.
Andere Begriffe für Accuracy sind Korrektklassifikationsrate oder Treffergenauigkeit.
Rechnerisch heißt das:
\[ \mbox{accuracy} = \frac{\mbox{korrekte Vorhersagen}}{\mbox{Anzahl aller Beispiele}} \]
Wenn wir das mit Hilfe unserer Begrifflichkeiten ausdrücken wollen, ist das:
\[ \mbox{accuracy} = \frac{TP + TN}{TP + TN + FP + FN} \]
Im Beispiel kommen wir auf eine Accuracy von 97.3%:
\[ \mbox{accuracy} = \frac{28 + 556}{28 + 556 + 12 + 4} = 0.973\]
Wie gesagt: Eine Besonderheit von Accuracy ist, dass auch Negatives stark in den Wert eingehen. Umgekehrt ist das nicht immer erwünscht, denn in der Regel gibt es deutlich mehr Negatives als Positives, so dass das Ergebnis von Accuracy weniger aussagekräftig ist. Daher ist bei binärer Klassifikation immer zu überlegen, ob nicht Precision und Recall geeignetere Maße sind.
Ein Vorteil von Accuracy ist, dass sie bei der Mehrklassen-Klassifikation relativ leicht umsetzbar ist (im Gegensatz zu Precision und Recall), wie wir später noch sehen werden.
6.3 Keras-Beispiel für binäre Klassifikation
Damit Sie die Mechanismen in Python sehen, bauen wir uns ein einfaches Neuronales Netz.
Als Datensatz verwenden wir die MNIST-Daten, die wir aus Abschnitt 5.4 kennen. Der Datensatz enthält kleine 28x28-Bilder der Ziffern 0 bis 9. Der Input besteht also aus 784 Pixelwerten, der Output aus einer Zahl aus {0, …, 9}.
MNIST hat eigentlich 10 Klassen, aber wir bauen zunächst einen binären Klassifizierer, der die Ziffer “5” erkennt (Output: 1 oder True), alle anderen Ziffern sind Fehlbeispiele (Output: 0 oder False). Dazu müssen wir entsprechend die y-Werte umbauen.
from tensorflow.keras.datasets import mnist
# Daten laden
(x_train, y_train), (x_test, y_test) = mnist.load_data()
# Linearisieren und normalisieren
x_train = x_train.reshape(60000, 784)/255.0
x_test = x_test.reshape(10000, 784)/255.0
# Alle 5er auf Zielwert 1, alle anderen auf 0
y_train5 = (y_train == 5).astype("float32")
y_test5 = (y_test == 5).astype("float32")
print('x_train: ', x_train.shape)
print('x_test: ', x_test.shape)
print("y_train5: ", y_train.shape)
print("y_test5: ", y_test.shape)x_train: (60000, 784)
x_test: (10000, 784)
y_train5: (60000,)
y_test5: (10000,)Jetzt erstellen wir ein sehr einfaches Neuronales Netz mit nur einer Schicht. Die Eingabe besteht aus 784 Zahlen, die Ausgabe aus einem Neuron mit Sigmoid-Aktivierung.
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Input, Dense
model = Sequential()
model.add(Input(shape=(784,))) # 784 Eingabeneuronen
model.add(Dense(1, activation='sigmoid')) # ein Ausgabeneuron
model.summary()Model: "sequential_2"
┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓ ┃ Layer (type) ┃ Output Shape ┃ Param # ┃ ┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩ │ dense_2 (Dense) │ (None, 1) │ 785 │ └─────────────────────────────────┴────────────────────────┴───────────────┘
Total params: 785 (3.07 KB)
Trainable params: 785 (3.07 KB)
Non-trainable params: 0 (0.00 B)
Wir trainieren für 10 Epochen mit SGD. Bei binärer Klassifikation verwenden wir die Verlustfunktion “Binary Crossentropy”, siehe auch Abschnitt 4.2.1.1.
model.compile(optimizer='sgd',
loss='binary_crossentropy',
metrics=['acc'])import time
start_time = time.time()
history1 = model.fit(x_train, y_train5,
epochs=10,
validation_data = (x_test, y_test5))
duration = time.time() - start_time
print(f'TRAININGSDAUER: {duration:.2f} Sek.')Epoch 1/10
1875/1875 ━━━━━━━━━━━━━━━━━━━━ 1s 475us/step - acc: 0.9163 - loss: 0.2327 - val_acc: 0.9503 - val_loss: 0.1430
Epoch 2/10
1875/1875 ━━━━━━━━━━━━━━━━━━━━ 1s 454us/step - acc: 0.9487 - loss: 0.1464 - val_acc: 0.9594 - val_loss: 0.1236
Epoch 3/10
1875/1875 ━━━━━━━━━━━━━━━━━━━━ 1s 424us/step - acc: 0.9554 - loss: 0.1305 - val_acc: 0.9627 - val_loss: 0.1150
Epoch 4/10
1875/1875 ━━━━━━━━━━━━━━━━━━━━ 1s 412us/step - acc: 0.9584 - loss: 0.1233 - val_acc: 0.9643 - val_loss: 0.1100
Epoch 5/10
1875/1875 ━━━━━━━━━━━━━━━━━━━━ 1s 414us/step - acc: 0.9628 - loss: 0.1149 - val_acc: 0.9660 - val_loss: 0.1064
Epoch 6/10
1875/1875 ━━━━━━━━━━━━━━━━━━━━ 1s 406us/step - acc: 0.9622 - loss: 0.1167 - val_acc: 0.9671 - val_loss: 0.1040
Epoch 7/10
1875/1875 ━━━━━━━━━━━━━━━━━━━━ 1s 407us/step - acc: 0.9639 - loss: 0.1113 - val_acc: 0.9677 - val_loss: 0.1019
Epoch 8/10
1875/1875 ━━━━━━━━━━━━━━━━━━━━ 1s 425us/step - acc: 0.9645 - loss: 0.1100 - val_acc: 0.9680 - val_loss: 0.1003
Epoch 9/10
1875/1875 ━━━━━━━━━━━━━━━━━━━━ 1s 429us/step - acc: 0.9643 - loss: 0.1083 - val_acc: 0.9693 - val_loss: 0.0990
Epoch 10/10
1875/1875 ━━━━━━━━━━━━━━━━━━━━ 1s 461us/step - acc: 0.9663 - loss: 0.1064 - val_acc: 0.9693 - val_loss: 0.0980
TRAININGSDAUER: 8.44 Sek.Die originale Ausgabe sieht so aus:
pred = model.predict(x_test)
pred[:5]313/313 ━━━━━━━━━━━━━━━━━━━━ 0s 234us/steparray([[0.0031052 ],
[0.1383998 ],
[0.01600501],
[0.00218798],
[0.00102575]], dtype=float32)Damit wir die Werte für die Konfusionsmatrix mit den Zielwerten vergleichen können, bilden wir sie mit Hilfe eines Schwellwerts von 0.5 auf 0 oder 1 ab.
y_pred5 = [(1 if x>=0.5 else 0) for x in pred]
y_pred5[:20][0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0]6.3.1 Konfusionsmatrix
Wir hatten auf den Testdaten die Vorhersagen berechnet und lassen uns jetzt die Konfusionsmatrix berechnen. Dazu übergeben wir die wahren y-Werte und die vom Modell verhergesagten y-Werte.
Siehe confusion_matrix bei scikit-learn.
from sklearn import metrics
cm = metrics.confusion_matrix(y_test5, y_pred5)
cmarray([[9037, 71],
[ 236, 656]])Wir visualisieren die Konfusionsmatrix mit Hilfe der Library Seaborn.
Siehe seaborn.heatmap bei seaborn.
import seaborn as sns
import pandas as pd
sns.heatmap(pd.DataFrame(cm), annot=True, cmap="YlGnBu", fmt='d')
plt.tight_layout()
plt.title('Verwechslungsmatrix', y=1.1)
plt.ylabel('Korrektes Label')
plt.xlabel('Vorhergesagtes Label')Text(0.5, 23.52222222222222, 'Vorhergesagtes Label')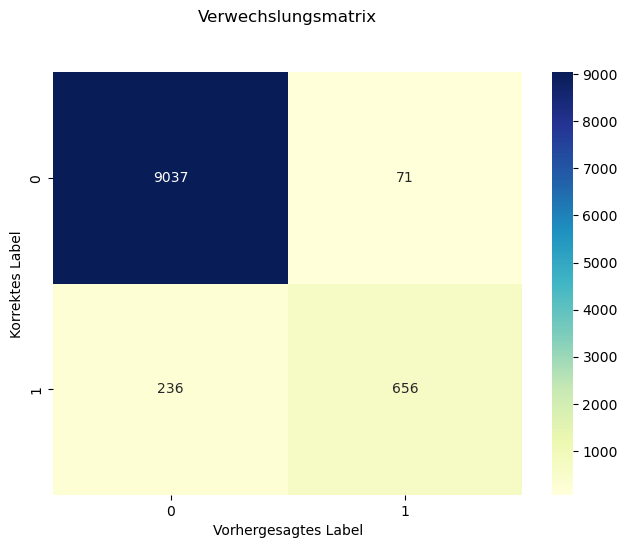
6.3.2 Precision, Recall und Accuracy
Anhand der Werte in der Matrix belegen wir Variablen TN, TP, FP und FN.
TN = 9037
TP = 656
FP = 71
FN = 236Mit diesen Werten können wir Precision, Recall und Accuracy anhand der Formeln berechnen.
print("Precision: ", TP / (TP + FP))Precision: 0.9023383768913342print("Recall: ", TP / (TP + FN))Recall: 0.7354260089686099print("Accuracy: ", (TP+TN)/(TP+TN+FP+FN))Accuracy: 0.9693Diese Funktionen werden auch in Scikit-learn bereitgestellt. Daher benutzen wir fortan die eingebauten Funktionen.
Siehe recall_score und precision_score bei scikit-learn.
print("Precision:", metrics.precision_score(y_test5, y_pred5))
print("Recall:", metrics.recall_score(y_test5, y_pred5))
print("Accuracy:", metrics.accuracy_score(y_test5, y_pred5))Precision: 0.9023383768913342
Recall: 0.7354260089686099
Accuracy: 0.96936.4 Mehrklassen-Klassifikation
Bei mehreren Klassen können wir auch eine Konfusionsmatrix aufstellen. Abbildung 6.1 zeigt eine Konfusionsmatrix mit drei Klassen A, B und C.
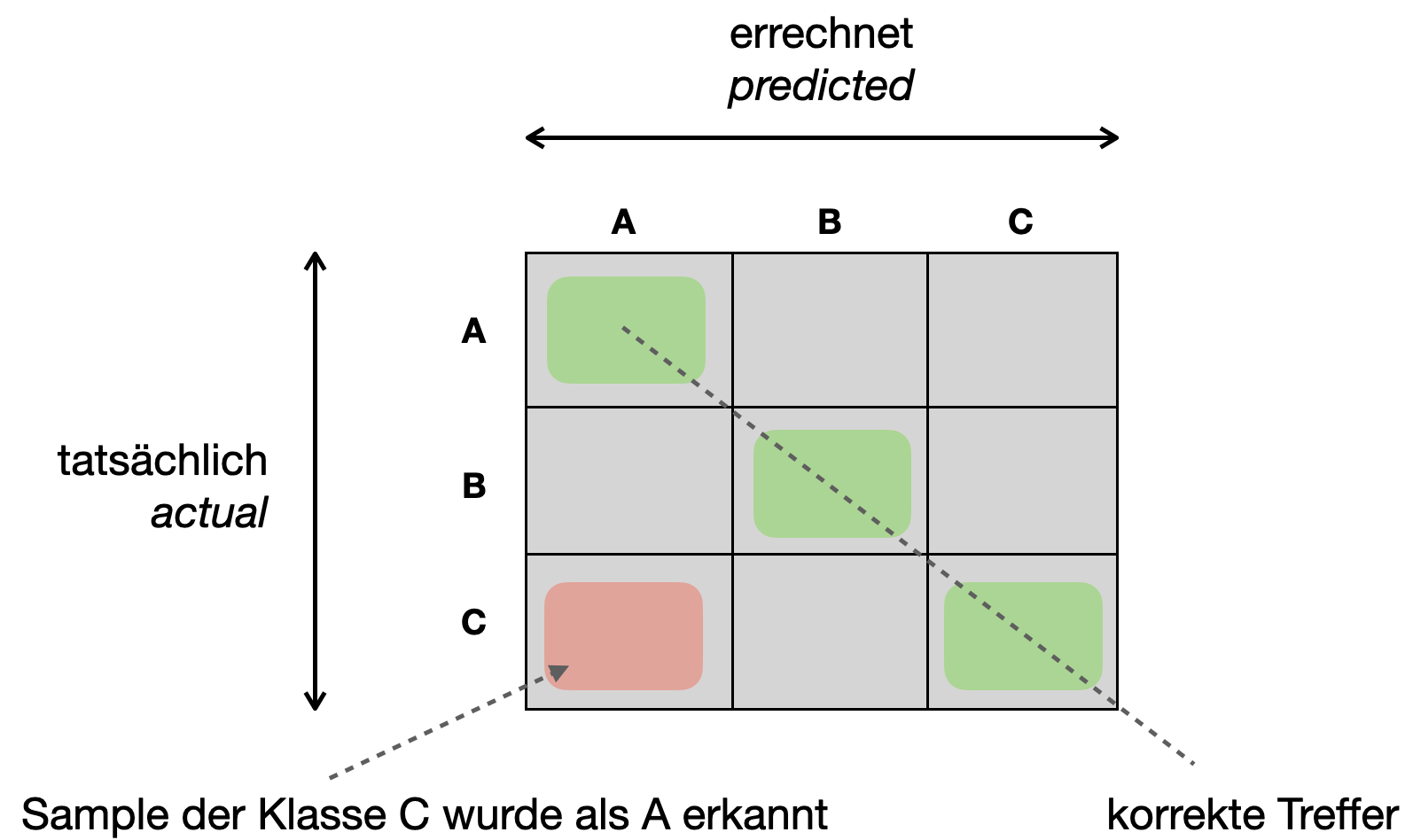
Auch hier finden wir auf der Diagonalen alle korrekten Vorhersagen. In den anderen Zellen können wir genau ablesen, welche Klasse mit welcher verwechselt wurde.
6.4.1 Accuracy
Bei der Mehrklassen-Klassifikation kann man nicht mehr von True Positives, False Positives etc. sprechen, denn es gibt nicht mehr die binäre Unterteilung in zwei Klassen (Positives, Negatives). Für die Berechnung der Accuracy ist das aber nicht weiter schlimm. Mit Hilfe der Konfusionsmatrix kann Accuracy direkt berechnet werden:
\[ \mbox{accuracy} = \frac{\mbox{Summe aller Diagonalzellen}}{\mbox{Summe aller Zellen}} \]
Denn das entspricht der Definition
\[ \mbox{accuracy} = \frac{\mbox{korrekte Vorhersagen}}{\mbox{Anzahl aller Beispiele}} \]
Natürlich benötigt man nicht unbedingt die Konfusionsmatrix zur Berechnung. Man kann einfach den entsprechenden Datensatz durchlaufen, die korrekten Vorhersagen zählen und dies am Schluss durch die Größe des Datensatzes teilen.
Da es im Machine Learning oft um Mehrklassen-Klassifikation geht, trifft man dort Accuracy am häufigsten als Maß an, da es relativ leicht zu berechnen ist.
6.4.2 Recall und Precision
Die Metriken Precision und Recall lassen sich nicht ohne weiteres von binärer Klassifikation auf mehrere Klassen übertragen. Stattdessen berechnet man für jede Klasse das entsprechende Maß, als wäre es ein binäres Problem (Klasse vs. Rest) und bildet anschließend den Mittelwert über alle Klassen.
Zum Beispiel kann man für Kategorie A die Precision \(P_A\) für Klasse A versus nicht-A berechnen. Das kann man sich anhand der Konfusionsmatrix verdeutlichen, wo wir die Zellen für B und C zu “nicht A” zusammenfassen. Dann haben wir wieder die Werte für TP, FP, TN und FN und können Precision aus der Sicht von Klasse A berechnen.
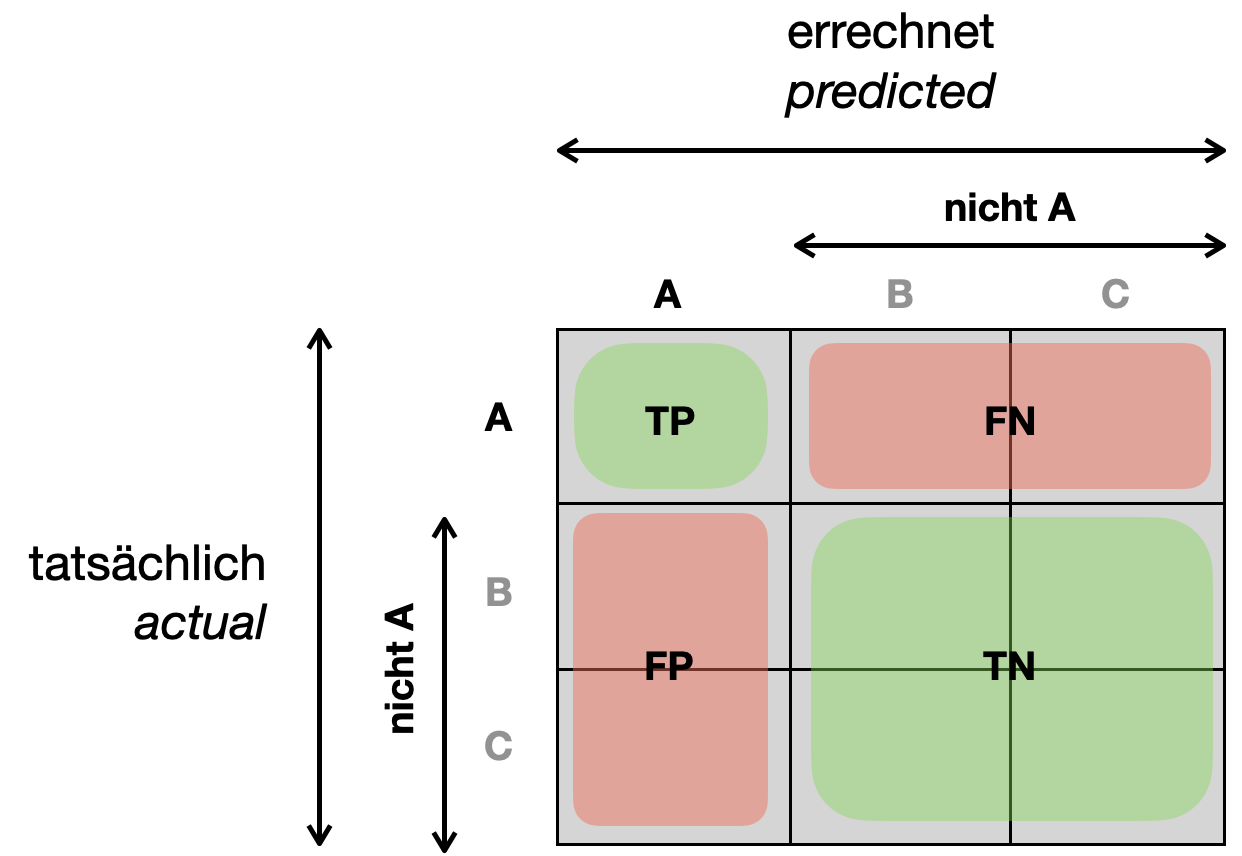
Dasgleiche können wir für B und C tun, um \(P_B\) und \(P_C\) zu berechnen. Die gesamte Precision ist dann der Mittelwert:
\[P = \frac{P_A + P_B + P_C}{3}\]
Jetzt kann man auf die Idee kommen, dass eine Klasse, die häufiger vertreten ist, auch mit mehr Gewicht in das Gesamtmaß eingebracht werden soll. Nehmen wir an die Klassen A, B, C sind mit je 50%, 30%, 20% in den Samples vertreten.
Dann wäre ein gewichtetes Mittel wie folgt:
\[P_{weighted} = 0.5 \,P_A + 0.3\,P_B + 0.2\,P_C\]
6.5 Keras-Beispiel mit mehreren Klassen
Jetzt verwenden wir alle 10 Klassen der MNIST-Daten und trainieren ein Neuronales Netz damit. Dazu wandeln wir die Zielwerte in One-Hot-Vektoren um.
from tensorflow.keras.utils import to_categorical
y_train = to_categorical(y_train, 10)
y_test = to_categorical(y_test, 10)
print("y_train: ", y_train.shape)
print("y_test: ", y_test.shape)y_train: (60000, 10)
y_test: (10000, 10)Jetzt erstellen wir wieder ein sehr einfaches Netz. Es hat 10 Ausgabeneuronen mit Softmax-Aktivierung.
model = Sequential()
model.add(Input(shape=(784,)))
model.add(Dense(10,
activation='softmax'))
model.summary()Model: "sequential_1"
┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓ ┃ Layer (type) ┃ Output Shape ┃ Param # ┃ ┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩ │ dense_1 (Dense) │ (None, 10) │ 7,850 │ └─────────────────────────────────┴────────────────────────┴───────────────┘
Total params: 7,850 (30.66 KB)
Trainable params: 7,850 (30.66 KB)
Non-trainable params: 0 (0.00 B)
Beim Training verwenden wir SGD und diesmal die Verlustfunktion “Categorical Crossentropy”, siehe auch Abschnitt 4.2.1.2.
model.compile(optimizer='sgd',
loss='categorical_crossentropy',
metrics=['acc'])
start_time = time.time()
history = model.fit(x_train, y_train,
epochs=10,
validation_data = (x_test, y_test))
duration = time.time() - start_time
print(f'TRAININGSDAUER: {duration:.2f} Sek.')Epoch 1/10
1875/1875 ━━━━━━━━━━━━━━━━━━━━ 1s 447us/step - acc: 0.7016 - loss: 1.1575 - val_acc: 0.8818 - val_loss: 0.4823
Epoch 2/10
1875/1875 ━━━━━━━━━━━━━━━━━━━━ 1s 387us/step - acc: 0.8767 - loss: 0.4780 - val_acc: 0.8956 - val_loss: 0.4011
Epoch 3/10
1875/1875 ━━━━━━━━━━━━━━━━━━━━ 1s 387us/step - acc: 0.8908 - loss: 0.4076 - val_acc: 0.9043 - val_loss: 0.3683
Epoch 4/10
1875/1875 ━━━━━━━━━━━━━━━━━━━━ 1s 390us/step - acc: 0.8955 - loss: 0.3854 - val_acc: 0.9074 - val_loss: 0.3486
Epoch 5/10
1875/1875 ━━━━━━━━━━━━━━━━━━━━ 1s 388us/step - acc: 0.8989 - loss: 0.3640 - val_acc: 0.9096 - val_loss: 0.3365
Epoch 6/10
1875/1875 ━━━━━━━━━━━━━━━━━━━━ 1s 387us/step - acc: 0.9044 - loss: 0.3476 - val_acc: 0.9114 - val_loss: 0.3269
Epoch 7/10
1875/1875 ━━━━━━━━━━━━━━━━━━━━ 1s 445us/step - acc: 0.9075 - loss: 0.3419 - val_acc: 0.9118 - val_loss: 0.3204
Epoch 8/10
1875/1875 ━━━━━━━━━━━━━━━━━━━━ 1s 422us/step - acc: 0.9077 - loss: 0.3322 - val_acc: 0.9147 - val_loss: 0.3144
Epoch 9/10
1875/1875 ━━━━━━━━━━━━━━━━━━━━ 1s 386us/step - acc: 0.9109 - loss: 0.3230 - val_acc: 0.9143 - val_loss: 0.3106
Epoch 10/10
1875/1875 ━━━━━━━━━━━━━━━━━━━━ 1s 398us/step - acc: 0.9110 - loss: 0.3203 - val_acc: 0.9154 - val_loss: 0.3059
TRAININGSDAUER: 7.97 Sek.Damit wir eine Konfusionsmatrix bilden können, müssen wir die One-Hot-Vektoren wieder in Zahlen umwandeln. Dazu verwenden wir die argmax-Operation (siehe Abschnitt 3.2.3 zu argmax).
import numpy as np
y_pred = model.predict(x_test)
y_pred_num = np.argmax(y_pred, axis=1)
y_test_num = np.argmax(y_test, axis=1)
y_pred_num313/313 ━━━━━━━━━━━━━━━━━━━━ 0s 262us/steparray([7, 2, 1, ..., 4, 5, 6])6.5.1 Konfusionsmatrix
Jetzt berechnen wir die Konfusionsmatrix, die bei 10 Klassen die Form 10x10 hat.
cm = metrics.confusion_matrix(y_test_num, y_pred_num)
cmarray([[ 961, 0, 2, 2, 1, 2, 9, 1, 2, 0],
[ 0, 1105, 2, 3, 0, 3, 4, 1, 17, 0],
[ 10, 7, 906, 16, 14, 1, 13, 15, 41, 9],
[ 4, 0, 23, 915, 0, 27, 2, 11, 17, 11],
[ 1, 2, 5, 2, 913, 1, 11, 3, 8, 36],
[ 11, 4, 6, 42, 11, 756, 14, 8, 31, 9],
[ 14, 3, 3, 3, 13, 13, 905, 2, 2, 0],
[ 2, 12, 26, 6, 7, 0, 0, 936, 2, 37],
[ 6, 11, 8, 24, 9, 22, 13, 12, 855, 14],
[ 11, 7, 3, 12, 40, 9, 0, 20, 5, 902]])Wir visualisieren die Matrix mit Seaborn.
sns.heatmap(pd.DataFrame(cm), annot=True, cmap="YlGnBu", fmt='d')
plt.tight_layout()
plt.title('Verwechslungsmatrix', y=1.1)
plt.ylabel('Korrektes Label')
plt.xlabel('Vorhergesagtes Label')Text(0.5, 23.52222222222222, 'Vorhergesagtes Label')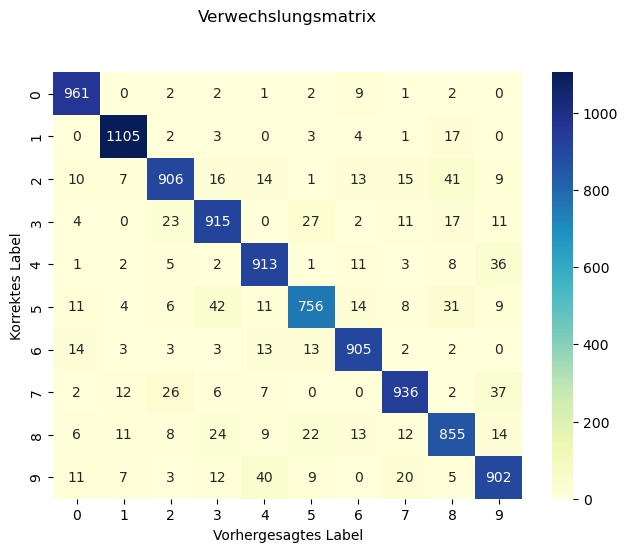
6.5.2 Accuracy
Jetzt berechnen wir die Accuracy über alle Klassen.
acc = metrics.accuracy_score(y_test_num, y_pred_num)
print(f"Accuracy: {acc:.3f}")Accuracy: 0.9156.5.3 Precision und Recall
Precision und Recall werden hier für jede Kategorie einzeln berechnet (0 vs nicht-0, 1 vs nicht-1, 2 vs nicht-2 usw.). Anschließend werden die 10 Werte gemittelt.
precision = metrics.precision_score(y_test_num, y_pred_num, average='macro')
recall = metrics.recall_score(y_test_num, y_pred_num, average='macro')
print(f"Precision: {precision:.4f}")
print(f"Recall: {recall:.4f}")Precision: 0.9146
Recall: 0.9142Mit der Option average=‘weighted’ wird der Mittelwert gewichtet, je nachdem wie hoch der Anteil der jeweiligen Kategorie ist.
precision = metrics.precision_score(y_test_num, y_pred_num, average='weighted')
recall = metrics.recall_score(y_test_num, y_pred_num, average='weighted')
print(f"Precision: {precision:.4f}")
print(f"Recall: {recall:.4f}")Precision: 0.9153
Recall: 0.9154Bei den MNIST-Daten ist jede Klasse gleich oft vertreten, daher sind Mittelwert und gewichteter Mittelwert gleich (Rundungsabweichungen können auftreten). Wenn man eine sehr ungleiche Verteilung hat, sollte man aber das gewichtete Mittel in Betracht ziehen. Ein anderer Fall ist, dass eine Klasse besonders wichtig ist, z.B. bei automatischer Mailklassifizierung die Klasse “Beschwerde”.
6.6 Cross-Valididierung
Holdout-Daten (egal ob Validierungsdaten oder Testdaten) sind natürlich für das Training “verloren”. Man könnte überlegen, dass man genau die “falschen” Daten für das Testen zurückhält, oder dass man zu viele oder zu wenige nimmt. Schließlich möchte man für das Training möglichst viele und möglichst “gute” Daten verwenden.
6.6.1 N-Fold Cross-Validation
Ein Verfahren, um die obigen Bedenken abzuschwächen, ist Cross-Validation (im Deutschen auch “Kreuzvalidierung”, aber der englische Begriffe ist üblicher). Die Grundidee ist, dass man in mehreren Runden immer andere Validierungsdaten benutzt, und am Ende die jeweils gemessene Performanz mittelt. Wir nehmen hier als Performanzmaß die Accuracy, es könnte aber auch der Fehler (Loss), Precision oder Recall sein.
Wir demonstrieren das hier mit 5-fold cross validation (5-fold CV). Man teilt die Trainingsdaten zufällig in fünf Teile (auch “folds” genannt) \(D_1, \ldots, D_5\) mit je 20% der Daten. Natürlich sind die fünf Teilmengen nicht-überlappend (man sagt auch disjunkt).
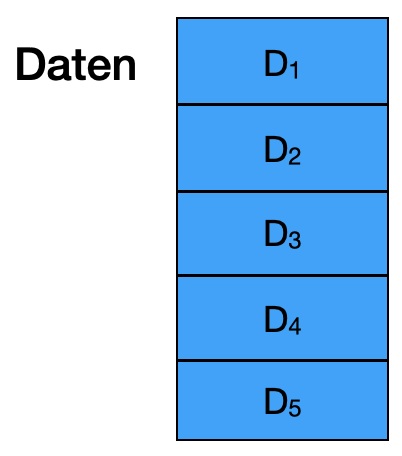
Die Grundidee ist jetzt, dass man in fünf Durchläufen immer einen andere Teilmenge als Testdaten nimmt. Zunächst wählt man \(D_5\) als Testdatensatz und trainiert auf \(D_1, \ldots, D_4\). Man misst die Accuracy entsprechend auf \(D_5\). In der nächsten Runde setzt man das Netz komplett zurück und training neu.
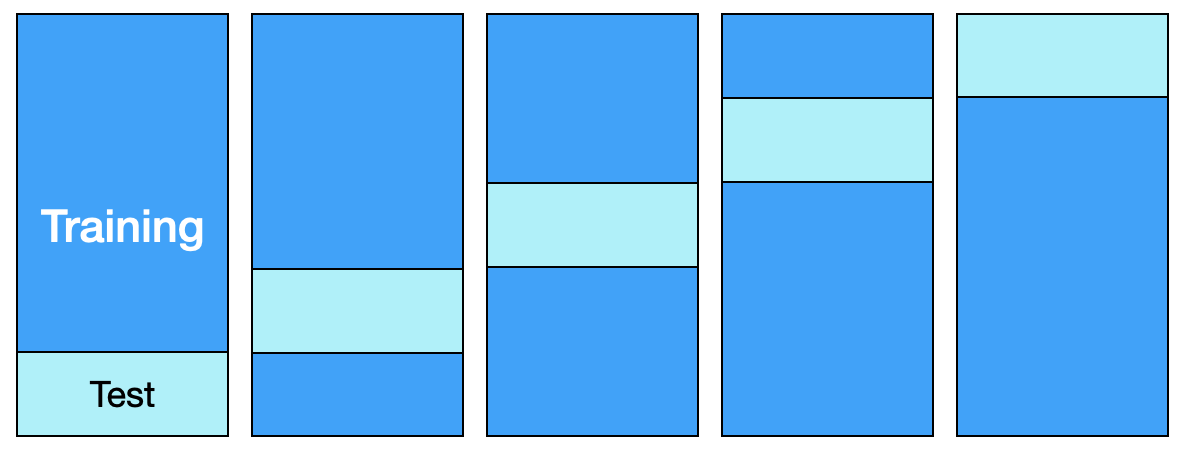
Wir schauen uns alle fünf Durchläufe mit der entsprechenden Aufteilung und Messung der Accuracy an:
- Training auf \(D_1, D_2, D_3, D_4\), Test auf \(D_5\) => Accuracy \(Acc_1\)
- Training auf \(D_1, D_2, D_3, D_5\), Test auf \(D_4\) => Accuracy \(Acc_2\)
- Training auf \(D_1, D_2, D_4, D_5\), Test auf \(D_3\) => Accuracy \(Acc_3\)
- Training auf \(D_1, D_3, D_4, D_5\), Test auf \(D_2\) => Accuracy \(Acc_4\)
- Training auf \(D_2, D_3, D_4, D_5\), Test auf \(D_1\) => Accuracy \(Acc_5\)
Die Gesamt-Accuracy ist dann der Durchschnitt \(\frac{1}{5} \sum_i Acc_i\).
6.6.2 Leave-One-Out
Ein Extremfall der Cross-Validierung ist die Leave-One-Out-Methode. Hier wird in jeder Runde nur ein Validierungsbeispiel aus dem Trainingsdatensatz herausgehalten (leave one out). Bei 100 Trainingsbeispielen wird also 1 Beispiel herausgehalten und auf den restlichen 99 Beispielen trainiert. Anschließend wird auf dem einen Validierungsbeispiel gemessen. In den nächsten 99 Runden wird das gleiche mit jeweils anderen Beispielen wiederholt und am Ende werden die 100 Werte gemittelt. Bei \(N\) Trainingsbeispielen entspricht Leave-One-Out also einer N-fold cross validation.
6.6.3 Relevanz für Deep Learning
Aktuell wird im Bereich des Deep Learning allerdings eher selten Cross-Validation angewendet, weil das Verfahren mit einem Mehraufwand verbunden ist: Bei K-fold cross validation vervielfacht sich die Trainingsdauer um Faktor K. Umgekehrt ist das Problem, dass Validierungsdaten “verloren” gehen, gerade bei großen Datenmengen eher marginal.
Umgekehrt ist Cross-Validierung im Bereich Machine Learning, auch z.B. auf Plattformen wie Kaggle, sehr üblich, denn es gibt in den entsprechenden Bibliotheken (z.B. scikit-learn) vorgefertigte Funktionen und Mechanismen, um Cross-Validierung relativ leicht umzusetzen. Es könnte eine Rolle spielen, dass die populären Methoden im allgemeinem ML-Bereich (z.B. Random Forests oder Gradient Boosting) nicht ganz so rechenintensiv sind wie die meisten Deep-Learning-Verfahren.
6.7 Maße ROC und AUC (optional)
Im Machine Learning findet man neben Recall, Precision und Accuracy zwei weitere Maße, um Modelle zu evaluieren:
- ROC: receiver operating characteristic
- AUC: area under the (ROC) curve
Hierbei ist AUC direkt von ROC abgeleitet.
Betrachten wir binäre Klassifikation als Szenario. Alle Verfahren geben als Output einen numerischen Wert, z.B. zwischen 0 und 1 aus. Mit Hilfe eines Schwellwerts wird dann entschieden, ob das Modell sich für Klasse A oder Nicht-A entscheidet. Oft ist dieser Schwellwert 0,5 - aber offensichtlich kann man den Wert auch anders wählen. Mit Schwellwert 0,8 werden weniger Fälle als A klassifiziert. Mit Schwellwert 0,1 werden fast alle Fälle als A klassifiziert.
Nun ist es so, dass man mit einem niedrigen Schwellwert einen hohen Recall erzielt. Im Extremfall - mit Schwellwert 0 - bekommt man garantiert 100% Recall. Umgekehrt leidet natürlich die Precision bei einem niedrigen Schwellwert. Man könnte also sagen: Wir suchen den optimalen Schwellwert, so dass Recall und Precision beide gut abschneiden. Die ROC-Kurve versucht, das abzubilden. Wir benutzen allerdings nicht direkt den Precision-Wert, sondern die False Positive Rate.
6.7.1 TPR und FPR
Wir betrachten also zwei Metriken für viele mögliche Schwellwerte ansehen: die True Positive Rate (TPR), welche identisch mit Recall ist, und die False Positive Rate (FPR), die zumindest mit der Idee der Precision verwandt ist.
TPR (= Recall) setzt - wie wir schon wissen - die korrekte Treffermenge ins Verhältnis zu allen Positives:
\[ \mbox{TPR} = \frac{TP}{TP + FN} = \frac{TP}{P} \]
FPR setzt die falsch klassifizierten Treffer (False Positives), die also eigentlich Negatives sind, ins Verhältnis zu allen Negatives:
\[ \mbox{FPR} = \frac{FP}{FP + TN} = \frac{FP}{N} \]
Für unser Corona-Beispiel bedeutet das: Eine hohe FPR heißt, dass vielen Getesteten fälschlicherweise gesagt wurde, sie hätten Corona. Der Unterschied zu Precision ist, dass hier ein hoher Wert quasi “schlecht” ist. Außerdem steht hier im Nenner die Gesamtzahl aller Negatives (beim Coronabeispiel ein sehr großer Wert), bei Precision steht im Nenner die Größe der Treffermenge (ein eher überschaubarer Wert).
6.7.2 ROC
Wenn wir unser Modell mit vielen unterschiedlichen Schwellwerten testen und für jeden Test FPR auf der x-Achse abtragen und TPR auf der y-Achse, erhalten wir die ROC-Kurve (receiver operating characteristic).
Schauen wir uns ein Beispiel an, wo wir ein Modell mit Hilfe von logistischer Regression trainiert haben.
Wenn wir einen Schwellwert von 1 anlegen, haben wir immer eine leere Treffermenge. Also bekommen wir einen Recall von 0%, also TPR = 0, aber wir haben auch keine False Positives, also FPR = 0.
Bei einem Schwellwert von 0,7 haben wir bei unserem Modell einen Recall von 50%, also TPR = 0,5. Wir bekommen aber auch ein paar False Positives, sagen wir FPR = 0,1.
Bei Schwellwert 0,5 liegt der Recall bei 80% (TPR = 0,8) und die FPR steigt auf 0,4.
Bei einem Schwellwert von 0 enthält die Treffermenge alle Datenpunkte, daher ist der Recall 100% (TPR = 1), aber wir haben auch so viele False Positives, wie theoretisch möglich sind, also FPR = 1.
Bei dem obigen Szenario, wo die Werte erfunden, aber plausibel sind, ergibt sich folgende “Kurve” mit den vier Datenpunkten. Diese Kurse ist die ROC-Kurve.
tpr = [0, 0.5, 0.8, 0.9, 1]
fpr = [0, 0.1, 0.2, 0.4, 1]
plt.plot(fpr, tpr, '-o')
plt.ylabel("True Positive Rate (TPR)")
plt.xlabel("False Positive Rate (FPR)")
plt.show()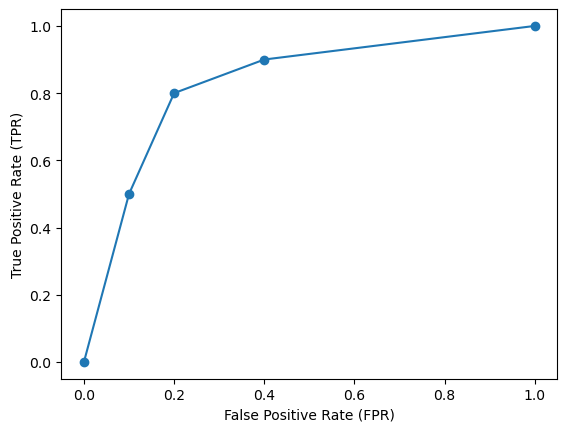
6.7.3 AUC
Je “bauchiger” die Kurve, umso besser die Performance des Modells, wohingegen eine Diagonale auf einen Zufallsprozess hindeutet. Dies wiederum messen wir mit dem Flächeninhalt AUC (area under the ROC curve).
Auf Wikipedia finden Sie unter Receiver operating characteristic diese Konzepte sehr schön erläutert.